Finding and correcting DC jumps


Sudden changes in the DC level are seen to occur within bolometer time streams. The following algorithm attempts to identify and correct these steps. Each bolometer time stream is processed independently using the following two part process

Part 1 - Detecting Candidate Steps:

In this part we search the bolometer time stream for contiguous blocks of samples that have unusually large gradients compared to the neighbouring samples. Each such block of samples is considered to be a candidate DC jump. The starting and ending time of each such block is noted. Once all candidate jumps have been found for a bolometer, the algorithm proceeds to part 2. Candidate jumps are found as follows:
  1. Smooth the bolometer time stream using a median filter of width DCSMOOTH (defaults to 50) samples. This reduces the effects of the noise in the data. Using a median filter rather than a mean filter helps to preserve the sharp edges at each DC jump, and is robust against spikes, etc. The following  figure shows a typical step, with  the original bolometer data values in red and the median-smoothed data values in blue.
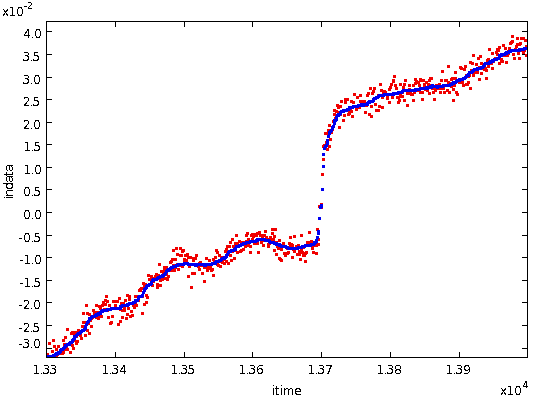
  2. At each sample, find the difference between the two adjacent values in the median filtered bolometer data. This is proportional to the gradient of the median filtered bolometer data. These gradients include both the gradient of the underlying noise free median-filtered data stream ,and the extra gradient caused by noise, spikes, DC jumps, etc. The following figure shows these differences for the above step. The high gradients at the step are clearly visible.
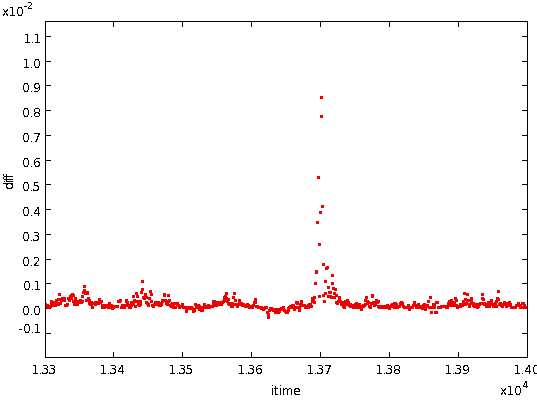
  3. We now need to split these differences up into differences caused by variation of the underlying  noise-free data, and differences caused by noise, steps, spikes, etc.To do this we smooth the above differences, and use the smoothed differences as the gradient of the underlying noise free data. In order to get an accurate result, we need to do this smoothing with a mean filter rather than a median filter. But a mean filter is badly affected by aberrant values, so we first take a copy of the differences found above, and remove extremely large differences by flagging them as bad. Specifically, differences more than three times the RMS difference (taken over the whole time stream) are set bad. The RMS is then re-calculated and a further two such rejection iterations are performed. This gets rid of  high gradient values caused by spikes, jumps, point sources, etc, leaving the following:
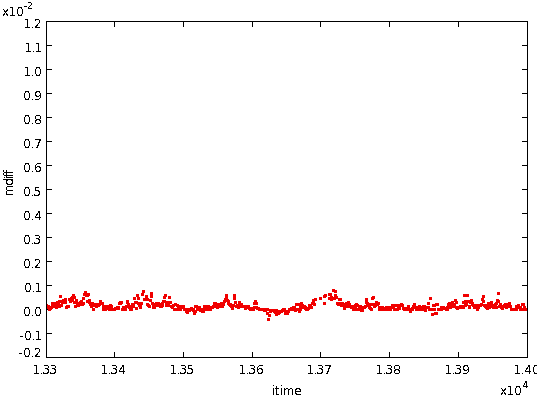
  4. The differences close to a step are often not typical of those in the wider neighbourhood, so each block of contiguous values removed above is doubled in width, leaving the following:

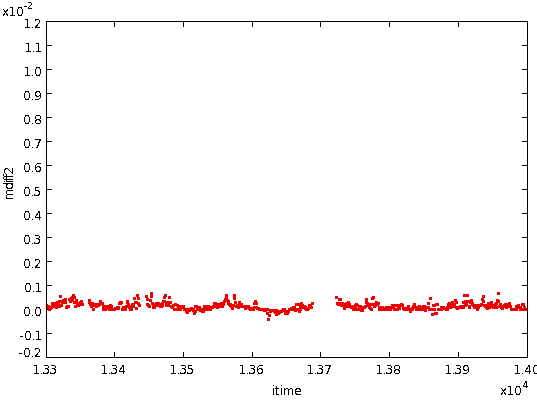
  5. Smooth the remaining differences using a mean filter of width DCSMOOTH.  The smoothing process fills in small holes in the array (up to 0.8*DCSMOOTH), but will not fill in larger holes. Such larger holes are filled in by linear interpolation. The resulting smoothed differences - shown in blue below overlayed on the original differences in red -  estimate the local gradient of the underlying noise-free median-filtered data stream.

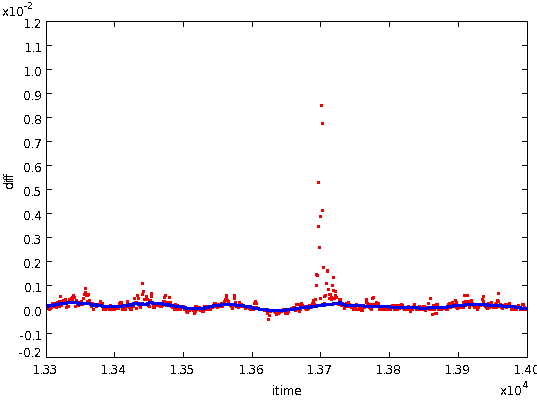
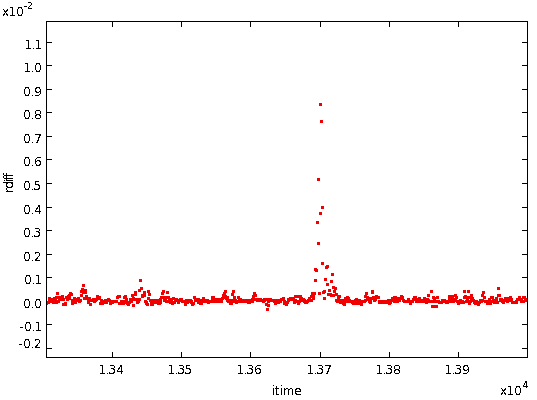
  6. Subtract the smoothed differences from the total differences found in step 2 above. This gives the residual differences caused by noise, spikes, DC jumps, etc., shown below:
  7. To decide if a residual difference value is "unusually high" we need an estimate of the local RMS of these residual differences at each point in the data stream. To get this we smooth the squared residual gradients using a median filter of width DCSMOOTH2 (fixed at 200), and then take the square root of the resulting values.
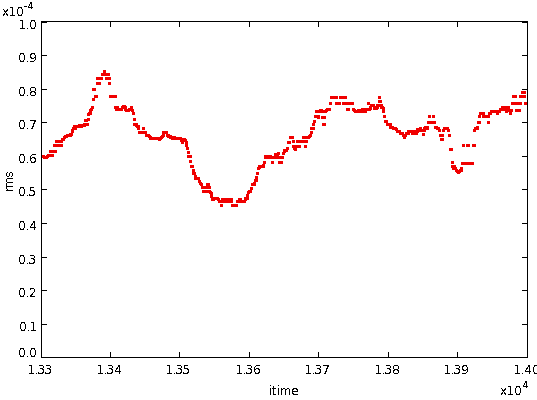
  8. Divide the residual differences by the local RMS of the residual differences to get a "signal-to-noise" ratio for each residual difference value:

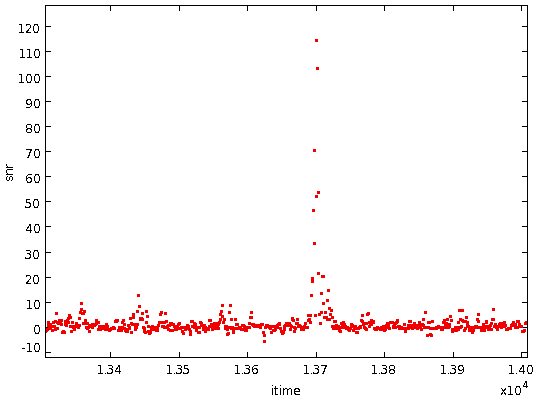
  9. Find all blocks of contiguous absolute SNR values greater than DCTHRESH (defaults to 25). Such blocks are allowed to contain small numbers of values that do not meet this criterion. The maximum length for such a section of low SNR is DCFILL (fixed at 40) samples. For the example step shown above, the block starts at 13696 and ends at 13703. Blocks are ignored if they fail any of the following tests:

Part 2 - Measuring and Correcting Steps

In this part, each of the candidate steps found above is processed to determine the height of the step.  This is done by doing a least squares linear fit to the median-smoothed bolometer data just before the step, and another fit to the data just after the step. These two fits are used to predict the value at the centre of the step, and the difference between these two predicted values is used as the step height. Various other tests are performed to identify and reject spurious step detections, and finally the original bolometer data stream is corrected to take out the step. For a given bolometer, each candidate step is processed as follows:
  1. Correct the step start and end to include adjacent SNR values that are below DCTHRESH but are still significantly high. Specifically, the step start is moved to the end of the last block of DCNLOW (fixed at 5) SNR values that are all less than DCSIGLOW (fixed at 8.0), and which occurs before the original step start. Likewise, the step end is moved to the start of the earliest block of DCNLOW SNR values that are all less than DCSIGLOW, and which occurs after the original step end.For the example step shown above, the start moves from 13696 to 13693, and the end moves from 13703 to 13711.
  2. Perform a linear fit to the median-smoothed bolometer data before the step. The fit is over a box containing DCFITBOX (defaults to30) samples. A gap of DCFITBOX samples is left between the end of the box and the start of the step.
  3. Perform a linear fit to the median-smoothed bolometer data after the step. The fit is over a box containing DCFITBOX samples, and a gap of DCFITBOX samples is left between the end of the step and the start of the box.
  4. These two fits are evaluated at the centre of the step. The difference between these values gives an estimate of the step height. However, moving the fitting box slightly can often result in big changes in the line gradient, and thus big changes to the estimate of the jump height. Steps where this is the case are ignored (i.e. left unfixed). To check this, more linear fits are performed at increasing distances from the step, and the consistency of the estimated jump heights from these extra fits is checked. Specifically, the fitting box used in step 2) above is moved one sample earlier, a new  fit is performed, and the new fit is used to estimate the value at the centre of the step.  The fitting box is then moved again by one sample and a third fit performed giving a third estimate of the central data value. This process is repeated until we have performed 2*DCFITBOX fits (an efficient algorithm is used to perform these multiple fits). The variance of all these estimates of the central value is found. The same thing is then done to the fit performed in step 3) above, to give us the variance of the central data value determined from the data following the step. The uncertainty in the jump height is then taken to be the square root of the mean of the two variances values, and the jump is ignored if the jump height - determined from steps 2) and 3) - is less than DCTHRESH2 (fixed at 1.5) times the uncertainty in the jump height.
  5. The jump is also ignored if it is less than DCTHRESH3 (fixed at 4.0) times the noise in the original bolometer data. The bolometer noise value used is the RMS of the differences between adjacent bolometer values, excluding aberrant points, and corrected by a factor of 1/sqrt(2).
  6. If the step is not rejected,  all the original bolometer values following the centre of the step are adjusted upwards or downwards by the step height.

Once all steps have been corrected, a constant value is added back on to all bolometer samples so that the original mean value in the bolometer is retained.